Как найти площадь трапеции

Что такое площадь трапеции и как её найти

Трапецией называется четырёхугольник, который имеет две параллельные и две непараллельные стороны. Площадь — это характеристика геометрической фигуры, которая показывает, сколько места она занимает на плоскости. Искать её можно по количеству квадратов, которые она вмещает.

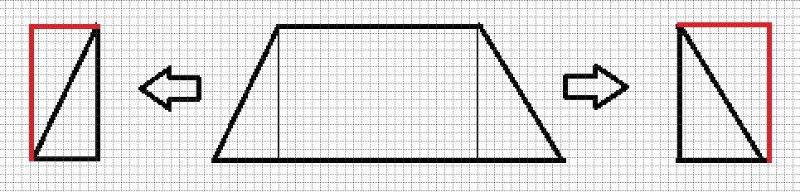
Для этого фигуру нужно разбить на прямоугольник и два треугольника. Затем треугольники необходимо достроить до прямоугольников, посчитать, сколько клеток в каждом из них, и разделить на 2. К полученному результату необходимо прибавить количество клеток в основном прямоугольнике. Это и будет искомая величина.  

Формулы для вычисления площади трапеции

Определять площадь трапеции по количеству квадратов неудобно. Это трудоёмкий и не всегда доступный для использования процесс. Поэтому для поиска искомой величины чаще применяют формулы.

Через основания и высоту

Основания — противоположные перпендикулярные стороны фигуры. А высота — это прямая, проведённая под прямым углом между его основаниями. Чтобы вычислить площадь, зная размеры этих элементов, умножьте сумму оснований на высоту и разделите на 2.

Формула нахождения площади трапеции:

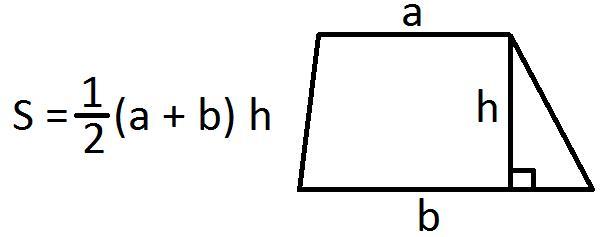
Пример. Известно, что трапеция имеет основания длиной 5 и 8 см, а её высота равна 6 см. Чтобы найти площадь, подставим эти данные в формулу: (5 + 8) × 6 ÷ 2 = 39 см². Площадь искомой фигуры составляет 39 см в квадрате.

Через высоту и среднюю линию

Средней называется линия, проведённая горизонтально между двумя боковыми сторонами фигуры. Умножив её на высоту, можно вычислить площадь трапеции.

В этом случае формула выглядит следующим образом:

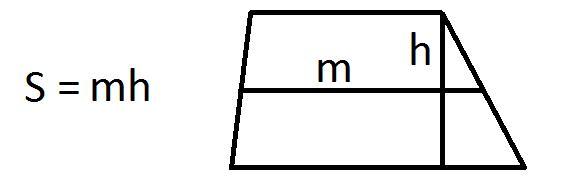
Пример. Высота трапеции равна 6 см, а длина её средней линии — 6,5 см. Вычислим искомую величину: 6,5 × 6 = 39 см².

Через диагонали и угол между ними

Диагональ — линия, соединяющая несмежные углы многоугольника. Зная размеры двух таких отрезков и величину угла, образованного при их пересечении, можно вычислить площадь трапеции. Она равна половине произведения диагоналей, умноженной на синус угла.

Формула нахождения площади через диагонали трапеции в геометрии:

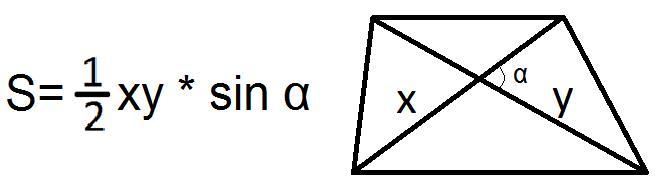
Пример. Известно, что диагонали трапеции составляют 6 и 8 см, а угол между ними равняется 30 градусам. Произведём расчёт рассматриваемым способом: 6 × 8 ÷ 2 × sin 30° = 24 × 0,5 = 12 см².

Через четыре стороны

Посчитать площадь трапеции этим методом сложнее. Но его используют, если известны длины четырёх сторон фигуры. В этом случае применяют формулу:

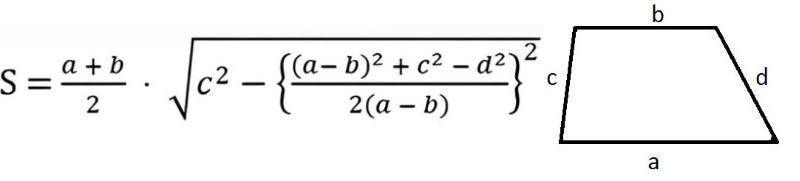
Пример. Известно, что, а = 10 см, b = 5 см, c = 4 см, d = 3 см. Чтобы рассчитать искомое значение, подставим эти величины в формулу:

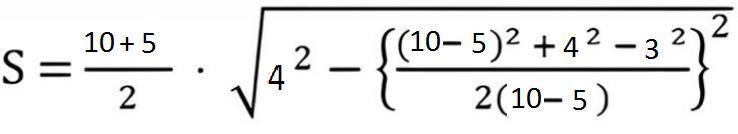
Осуществив все подсчёты, получим, что площадь трапеции равна 18 см².

Через радиус вписанной окружности и основания

Если в трапецию вписать окружность и узнать её радиус, можно найти площадь фигуры при известных размерах оснований. Для этого понадобится сложить длины оснований и умножить полученную сумму на радиус.

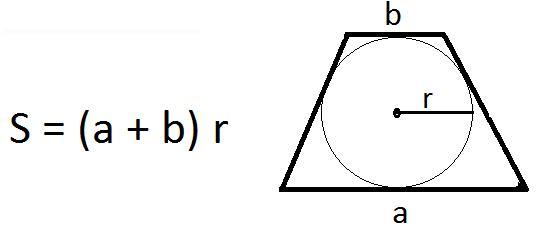
Пример. Возьмём трапецию с основаниями 4 и 7 см и радиусом вписанного в неё круга, равного 3 см. Вставим значения в формулу: (4 + 7) × 3 = 33 см². В этом произвольном примере площадь фигуры составила 33 квадратных сантиметра.

Равнобедренная трапеция

Равнобедренная или равнобокая — трапеция с одинаковыми боковыми сторонами. Особенные свойства такой фигуры — равенство её диагоналей, а также углов при каждом основании.

Вычисление по четырём сторонам

Площадь равнобокой трапеции по известным размерам её сторон находится следующим образом:

1. Вычтите из более длинного основания короткое и разделите полученную цифру на 2.
2. Вычислите квадрат полученного числа.
3. Из квадрата боковой стороны фигуры отнимите число, которое вы рассчитали на предыдущем этапе.
4. Определите корень полученного значения.
5. Умножьте его на сумму оснований и разделите на 2.

Формула расчёта выглядит так:

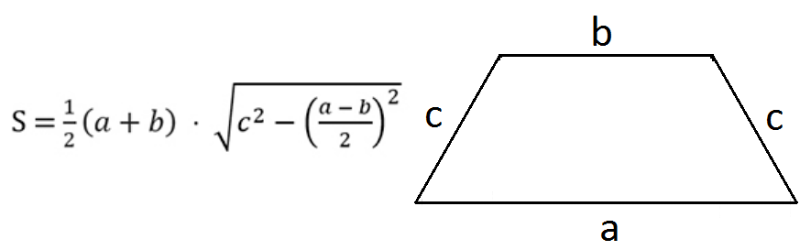
Вычисление по радиусу вписанной окружности и углу

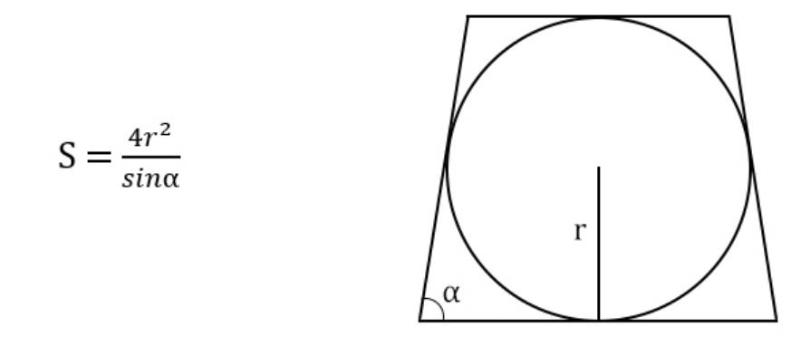
Чтобы найти площадь равнобедренной фигуры, зная радиус окружности и угол у основания трапеции, нужно:

1. Вычислить квадрат радиуса.
2. Умножить полученное значение на 4.
3. Разделить результат на синус угла.

Мы рассмотрели основные формулы, которые позволяют найти площадь трапеции. В литературе встречаются и другие способы, но они подходят для различных частных случаев.